Ces illusions sont souvent dues à des erreurs d'estimation, de dimension, d'interprétations, de courbure… par rapport à une figure géométrique.
Delboeuf, Hering, Müller-Jyer et beaucoup d'autres ont découvert, au cours de la seconde moitié du XIXe siècle, de nombreuses illusions géométriques qui portent souvent leur nom. Environ 200 illusions ont ainsi pu être répertoriées.
Une illusion géométrique comprend deux éléments : un élément qui provoque la déformation, appelé élément " inducteur " et un élément qui la subit, appelé élément " test ".
Les illusions géométriques naissent dans le système visuel, au niveau où convergent les informations venant de chaque œil.

Le cercle central de la figure de gauche paraît plus grand que celui de la figure de droite. Pourtant, ils sont identiques.

Un élément test entouré d'éléments inducteurs plus petits paraîtra plus grand que ce même élément test entouré d'éléments inducteurs plus grands.
Ceci est dû à un effet de contraste. Ce contraste apparaît quand la différence entre l'élément inducteur et l'élément test est grande.

Les trois lignes ont la même courbure malgré les apparences.

Les lignes obliques ne semblent pas parallèles alors qu'elles le sont.

Les illusions liées aux effets d'angles sont très nombreuses. On peut expliquer ces illusions à partir de deux principes. Tout d'abord, le principe d'orthogonalité. Nous avons tendance à vouloir ramener les angles vers des angles droit. Ainsi, nous surestimons les angles aigus et sous-estimons les angles obtus.

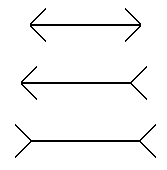La ligne droite du haut, à inflexions internes paraît plus courte que celle du bas, à inflexions externes.

Ensuite, le second principe est basé sur le fait que nous surestimons les côtés d'un angle obtus et, l'inverse, nous sous-estimons ceux d'un angle aigu.

Les lignes horizontale et verticale sont exactement de la même mesure.

Notre œil bouge plus vite à l'horizontal qu'à la verticale, ainsi, une ligne horizontale, paraît plus petite qu'une ligne, de la même longueur verticale.

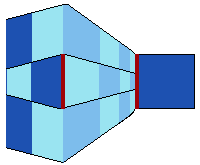Le trait rouge de droite paraît plus grand que celui de gauche. Cette illusion est renforcée par le damier.

Dans cette illusion de perspective, le cerveau interprète les lignes obliques comme des indicateurs de profondeur. Or, lorsque deux formes ont la même grandeur, celle paraissant la plus éloignée sera vue plus grande que l'autre et inversement.

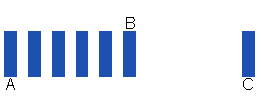La distance entre A et B paraît plus longue que la distance entre B et C.

Un espace divisé ou occupé par plusieurs éléments paraît souvent plus grand qu'un même espace vide.

Le haut du batonnet semble plus foncé que son autre extremité pourtant il n'est fait que d'une seule teinte.

En général, les couleurs d'arrière-plan influencent l'illusion. La lumière dépend de celle de l'objet lui-même mais aussi de son environnement lumineux.